归并排序及其应用

归并排序是一种典型的采用分治策略进行排序的算法，其中合并的过程用到了外部排序的方式，算法的时间复杂度可以通过master公式进行计算，空间复杂度为O(N)，本文我们来讨论一下归并排序的算法思路以及该算法适用的题型。

算法思路

归并排序的排序过程可以大体划分为两个阶段：划分阶段和合并阶段。并且根据每次对原序列划分的个数分为二路归并和多路归并两种，两者的区别仅仅在于划分的路数不同，本文以基本的二路归并为例进行研究。

划分阶段：将一个数组进行不断二分，直到将整个序列划分到单独一个元素为一部分为止
合并阶段：将相邻的划分好的部分进行合并，每次合并申请一个长度为要合并的两部分长度之和的数组作为辅助空间进行外部排序，排序好之后再将有序序列拷贝回这两个相邻的部分，即代表一次合并结束；不断合并直到合并到原序列

我们通过一个案例来分析这个过程，假设原序列为【2，0，7，3，8，5，4】，那么归并排序的过程大致如下：

划分过程：
1. 第一次划分：【2，0，7，3】；【8，5，4】
2. 第二次划分：【2，0】；【7，3】；【8，5】；【4】
3. 第三次划分：【2】；【0】；【7】；【3】；【8】；【5】；【4】

注意，这其中可能存在奇数偶数的问题，即划分过程不一定是很平均的，如果元素总个数为奇数个，那么必然会有一个元素提前一次划分完毕，成为单个部分。

合并过程：
1. 第一次合并：【0，2】；【3，7】；【5，8】
2. 第二次合并：【0，2，3，7】；【4，5，8】
3. 第三次合并：【0，2，3，4，5，7，8】

我们发现，合并和拆分正好是一个逆序的关系，且各个部分的划分与合并严格对应，在划分过程中被拆开的两个部分一定会在合并的阶段进行合并，这样的表现方式或许不够直观，通过下面这幅划分合并图我们可以看得更加清楚（图中不带箭头的实线表示划分过程，带箭头的实线表示合并过程）：

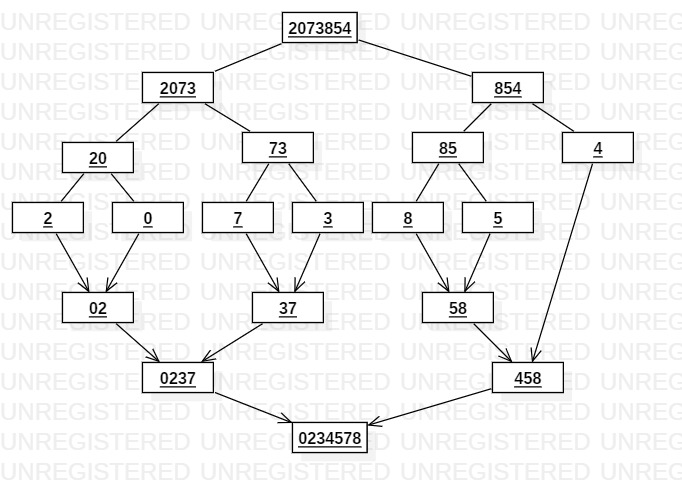
如图所示，每一层的代表一次划分或合并，从第二层开始依次是三次划分和三次合并。这里我们就可以直观的看出各个部分的划分与合并是严格对应的，第二次划分就单独成为一部分的元素4，在第一次的合并中就没有参与，而是直到倒数第二次合并才与其划分出来的85这个部分进行合并，由此我们可以得出两条推论，即在归并排序中：

第i次划分得到的两个部分在倒数第i次合并时才会进行合并
第i次划分时不需要再被划分的部分在倒数第i次合并中不会参与合并

代码解析

到目前为止，我们对归并排序的流程已经有了大致的把握，接下来就是函数实现的细节问题，例如边界值的判断，执行流程的控制等。从这个划分的过程来看，必然是一个递归函数的调用，在学习递归函数时我们说写一个递归函数，首先要考虑函数的终止条件，避免无休止的递归导致函数栈溢出，很显然这里的终止条件是划分的部分只有一个元素；第二步考虑递归的依赖条件，即我们想要完成对整个序列的排序，依赖于左半部分和右半部分的有序，同理左右两个部分的排序也依赖于其各自的左右两个部分的有序，以此类推……最终单个元素必然是有序的。
分析了这两方面的条件，我们来构造这个递归函数，为了便于函数参数的传递，我们将递归函数的参数设为本次划分出来的部分的首位下标，这样既便于函数的调用，也能够对base case作出判断；确定了函数的参数，接下来我们考虑是否需要返回值，显然我们的目的是对数组进行排序，而排序的过程可以在方法内完成，因此不需要返回值；函数内部流程我们可以抽象的分为下面几个步骤：

判断当前要排序的这个部分是否已经达到了终止条件，如果是则无需再进行排序，直接返回；否则在对其进行排序
将当前部分划分成左右两个部分，递归调用排序方法，使得左右两个子部分各自有序
将排序完成的左右两个部分通过外排的方式进行合并，使当前这个部分有序

根据上述分析，我们的代码如下：

/**
 * 归并排序算法
 * @param arr
 */
public static void mergeSort(int[] arr) {
	if(arr==null||arr.length<2)
		return;
	sortProcess(arr, 0, arr.length-1);
}
/**
 * 划分函数，二分
 * @param arr
 * @param left
 * @param right
 */
public static void sortProcess(int[] arr,int left,int right) {
	if(left==right)
		return;
	int middle = (left+right)/2;
	sortProcess(arr, left, middle);
	sortProcess(arr, middle+1, right);
	merge(arr, left, middle, right);
}

其中第一个函数是归并排序递归方法的第一个入口，同时对数组的可排序性进行了验证，我们也可以直接调用该方法的最后一行代码进入递归过程；而第二个递归函数的内部过程也和我们的分析过程如出一辙。这里对左右子序列的合并过程我们将其抽象出来，封装成一个函数，下面我们来讨论一下这个函数应当如何实现，前面我们说过归并的过程实际上是通过辅助数组来完成的，因为左右两个子部分通过递归调用排序方法已经达到有序，那么只需要两个指针从左右两个子部分的头开始，逐渐将两个子部分遍历一遍，每比较一次拷贝出一个小数，指针向后移动一下，直到某个部分的数全部拷贝完，再将另一部分剩余的数拷贝出来（最终再将辅助数组中的有序结果拷贝回原部分即可）。

假设现有有序的左右两个子部分【2,3,5】和【0,7,8】，则先申请一个长度为6的辅助数组【,,,,,】，合并的过程如下表所示：

阶段	左子部分	右子部分	辅助数组
比较拷贝	【2,3,5】	【~,7,8】	【0,,,,,_】
	【~,3,5】	【~,7,8】	【0,2,,,,】
	【,,5】	【~,7,8】	【0,2,3,,,_】
	【,,~】	【~,7,8】	【0,2,3,5,,】
补全拷贝	【,,~】	【,,8】	【0,2,3,5,7,_】
	【,,~】	【,,~】	【0,2,3,5,7,8】
拷回原序列	【0,2,3】	【5,7,8】	【0,2,3,5,7,8】

通过这个表格我们发现，在往辅助数组中拷贝元素时，必然存在某一个部分的元素提前拷贝完成的情况，但是不清楚数据情况的前提下我们是无法确定哪个部分会剩下元素的，因此我们需要在比较拷贝阶段结束后，再对两个部分进行判断和补全拷贝工作，这样才能保证每个元素都不会丢失，最终用辅助数组中的序列覆盖掉原数组中的序列即可。该方法的代码如下：

/**
 * 归并函数，复杂度为O(N)
 * @param arr
 * @param left
 * @param middle
 * @param right
 */
public static void merge(int[] arr, int left, int middle , int right) {
	int[] help = new int[right-left+1];
	int p = left, q = middle+1 , i = 0;
	//比较拷贝
	while(p<=middle&&q<=right)
		help[i++] = arr[p] < arr[q] ? arr[p++] : arr[q++];
	//补全拷贝
	//右子部分有剩余元素未拷贝结束
	while(q<=right)
		help[i++] = arr[q++];
	//左子部分有剩余元素未拷贝结束
	while(p<=middle)
		help[i++] = arr[p++];
	//拷回原序列
	for(i = 0 ; i < help.length ; i++)
		arr[left++] = help[i];
}

最后要注意写完算法之后使用对数器对该算法进行测试，避免边界值界定的失误导致代码出现漏洞。下面我们来分析一下算法的复杂度，空间复杂度很好判断，辅助数组只在每一次合并时申请，合并结束后直接释放，因此每一次合并不论分成多少个部分，其加起来的总和不会超过原数组的长度，这个通过观察上文中划分和合并图即可确定，合并的每一层各个部分都只不过是对原数组长度的划分，而辅助空间的申请也是依据子部分的长度，因此空间复杂度为O(N)。

注意，这里之所以说不会超过而不是直接说等于原数组的长度，是因为存在如上文中单个元素4的这种情况，这样就会使得某一次的合并时申请的空间没有原数组的长度那么长；

并且，也并非只有划分出单个元素会出现这种情况，工程应用中，子部分长度小于一定值时会直接对其使用插入排序（插入排序对样本量较少的序列时间成本更低），也会导致不再划分的情况

而对时间复杂度的判断我们就需要借助master公式进行求解，因为归并排序对于子过程的划分是相等的，这里忽略奇数个元素的情况，因为均分只估计规模不考虑常数。而不论是二路归并还是多路归并，其子部分划分的个数和总共要执行的子过程次数是一样的（一次划分过程中），因此a=b推出log(b,a)=1，同时通过观察合并函数，也可以发现剩余过程的时间复杂度是O(N)，因此d=1.由master公式我们可知，归并排序算法的时间复杂度为O(N*log(N))。

算法应用

学习归并排序不只是要了解该算法的实现和细节，更重要的是要掌握该算法的思想，能够将其灵活的运用到各种题目中。这里我们不妨反思一下为什么归并排序相比冒泡，选择，插入这三个O(N²)级别的算法时间复杂度更优，我们说排序无非是比较和交换两部分组成，当我们在比较数组中每个元素时，如果能将已经比较过的顺序关系重复利用，而不是重复比较，那么必然能节省更多的时间。反观冒泡，选择和插入这三个算法，每次遍历（比较）完整个序列只能确定一个数据的位置，下一次比较又要重头开始，等于之前比较的结果都浪费了，时间复杂度必然是差的。

反观归并排序，每一次子部分的排序结果都能在下一次合并的过程中用上，组内比较的次数是不会被浪费的，这是该算法时间复杂度较快的根本原因。

小和问题

题目：在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
举例：[1,3,4,2,5]
- 1左边比1小的数，没有；
- 3左边比3小的数， 1；
- 4左边比4小的数， 1、 3；
- 2左边比2小的数， 1；
- 5左边比5小的数， 1、 3、 4、 2；
- 所以小和为1+1+3+1+1+3+4+2=16
对数器：遍历整个数组，每个数的左边再遍历一遍，累加比当前数小的数，时间复杂度O(N²)
思路：小和的实质是要确定当前数的右边有多少个数比他大，借助归并排序可以加速这个过程。归并排序能够使得子部分的元素在组内有序，因此在两个子部分合并的过程中，一旦比较出左部分的某个元素（设为a）的值小于右部分的某个元素（设为b），通过与子部分右边界的下表变换即可确定右部分至少有几个元素的值比a大。且合并过程中，指针是从左往右依次遍历的，因此不会漏掉任何一个可累加的小和；每一个子部分合并完成时，该部分可以被榨取的小和全部榨取完成，在之后的合并过程中不会重复榨取，因此也不会多加任何一个小和。

下面我们根据题目的要求和解题思路来对归并算法做修改，首先大框架不变，依旧是划分和合并两个部分，不同的是这次我们要求小和，因此在合并的过程中不仅要将子部分排序，还要将榨取的小和返回回来进行累加。故递归函数和合并函数的返回值需要改为整型，相应的递归函数base case的返回值要改为0，因为单个元素的子部分不产生小和；而递归的依赖关系则是，整个序列的小和是通过左右两个子部分各自内部榨取的小和之和加上当前左右两个子部分之间可以榨取的小和得到的，因此递归调用过程是三个部分的累加和作为返回值，代码如下：

public static int smallSum(int[] arr) {
	if (arr == null || arr.length < 2)
		return 0;
	else
		return divide(arr, 0, arr.length - 1);
}

public static int divide(int[] arr, int left, int right) {
	if (left == right)
		return 0;
	else {
		int middle = left + ((right - left) >> 1);
		return divide(arr, left, middle) + divide(arr, middle + 1, right) + merge(arr, left, right, middle);
	}
}

下面考虑对合并函数的修改，其实相比归并排序中合并函数的功能，小和问题只需要在比较拷贝阶段榨取小和并最终返回即可，不涉及到其他代码逻辑的更改，因为小和是在比较的前提下产生的，而合并函数中只有比较拷贝阶段涉及左右两个子部分元素的比较。因此，我们需要在合并函数中增加一个累加小和的变量，并在比较阶段，对于左部分指针指向的值小于右部分指针指向的值时榨取小和，算法是由右部分指针下标和右子部分末端下标相减加一得出有多少个元素的值大于左部分指针指向的元素，相乘累加即可。代码如下：

public static int merge(int[] arr, int left, int right, int middle) {
	int[] help = new int[right - left + 1];
	int i = 0;
	int p = left;
	int q = middle + 1;
	int sum = 0;
	while (p <= middle && q <= right) {
		//榨取每个小组中的所有小和
		sum += arr[p] < arr[q] ? (right - q + 1) * arr[p] : 0;
		//先榨取后拷贝（指针后移）
		help[i++] = arr[p] < arr[q] ? arr[p++] : arr[q++];
	}
	while (p <= middle)
		help[i++] = arr[p++];
	while (q <= right)
		help[i++] = arr[q++];
	for (i = 0; i < help.length; i++) {
		arr[left + i] = help[i];
	}
	return sum;
}

我们看到，这道题的代码与归并排序的代码非常相似，且时间复杂度任然保持在O(N*log(N))，时间复杂度优于直接嵌套遍历查找，原因在于利用归并排序的思路求小和实质上是分批查找，而不是单个查找，每一次子部分合并，即可累加出一批小和，大大加速了查找效率。

逆序对问题

题目：在一个数组中，左边的数如果比右边的数大，则这两个数构成一个逆序对，请打印所有逆序对。
思路：延续小和问题的思路，在两个相对有序的子部分中，很容易知道某个数左右有几个大于或小于该数的元素，因此可以在合并的过程中比较左右两个指针指向的数的大小关系，符合逆序对时，左部分指针往后的数都是比当前数大的，故都能与右部分指针指向的数组成逆序对，故直接遍历输出即可。
代码修改：相比小和问题，本题对归并排序的代码改动更少，因为不涉及合并结果的累计，我们只需在合并时将符合条件的值输出即可，故只需在合并函数的比较拷贝阶段添加如下代码即可（注意以下代码要放在拷贝和指针后移之前执行）：

if(arr[p]>arr[q]) {
	for (int j = p; j <= middle; j++) {
		System.out.println("逆序对["+arr[j]+","+arr[q]+"]");
	}
}